
Katru šīs lapas vienumu izvēlējās House Beautiful redaktors. Mēs varam nopelnīt komisiju par dažām precēm, kuras jūs izvēlaties iegādāties.
Nekas tāds nav satraucoša matemātikas problēma, prāta locīšanas optiskā ilūzija, vai savīti loģikas mīkla apturēt visu produktivitāti Populārā mehānika birojs. Pēc dabas mēs esam ziņkārīgi cilvēki, bet arī mēs kolektīvi dalāmies spītīgā uzstājībā, ka esam pareizi, sasodīts, un tāpēc mums ir tendence nomest darbu malā, kad vien saskaramies ar problēmu, kas šķietami ir iespējama.
Šis trīsstūra smadzeņu ķircinātājs nav jauns - kliedziens uz Popsugar priekš atklājot to pirms pāris gadiem, bet, pamatojoties uz zināmu ēnas interneta burvību, šodien manā plūsmā parādījās zemāk esošais tvīts un uzsāka jaunas debates mūsu darbiniekiem Neierobežots kanāls - vieta, kas tradicionāli tiek rezervēta idejām par darbu veikšanu, bet to galvenokārt izmanto, lai kliegtu par citām lietām, par kurām ik pa laikam pārvēršamies saturs.
Sakiet? pic.twitter.com/lrhXrWw5EP
- J (@jiteshpillaai) 2018. gada 9. aprīlis
Tā kā esmu mazohists, es atkal uzzīmēju trīsstūri un palūdzu visiem darbiniekiem nekavējoties nomainīt to, ko viņi dara, un mēģināt atrisināt vienkāršo jautājumu: cik trijstūri jūs varat atrast?
Es jums saudzēšu pilnu sarunu - uzticieties man, neviens to negrib redzēt - bet komandas reakcija bija visur. Daži redaktori redzēja četrus trīsstūrus. Citi redzēja 12. Daži redzēja 6, 16, 22. Vēl vairāk redzēja 18. Viens gudrinieks pašā jautājumā saskaitīja trīsstūrus A rindās, bet otrs šķita, ka viņam ir eksistenciāls krīze: “Neviena no šīm līnijām nav patiesi taisna, tikai izliekta - tātad nevienu no tām nevar definēt kā trīsstūri,” viņš teica. “Šajā fotoattēlā nav trīsstūru. Dzīvei nav jēgas. ”
Pēc tam mēs izvirzījām problēmu mūsu Instagram sekotājiem, kuru atbildes arī ietvēra diapazonu, no 5. līdz 14. līdz 37. Kaut arī mēs atzīstam lielu vilkšanas varbūtību šeit, ir skaidrs, ka cilvēki uz problēmu reaģē daudz dažādos veidos.
Skatiet šo ziņu vietnē Instagram
Lūdzu, pārtrauciet to, ko jūs darāt, un palīdziet mums atrisināt debates, kas notiek mūsu birojā. Cik trijstūri jūs šeit redzat?
Ziņa, kuru kopīgoja Populārais žurnāls Mehānika (@popularmechanics) uz
Es visu dienu varētu noklausīties, kā mani kolēģi izskaidro viņu apšaubāmos procesus, bet tā vietā es sazinājos ar vairākiem ģeometrijas ekspertiem, lai noskaidrotu, vai mēs varam nonākt pie vienprātīgas atbildes. Izrādās, ka praktiski visi matemātiķi, ar kuriem es sazinājos, atrada to pašu risinājumu, bet ne visi viņi to izdomāja vienādi.
Ja nevēlaties vēl uzzināt atbildi, pārtrauciet lasīšanu un vispirms mēģiniet atrisināt problēmu. Es jūs satikšu šeit, kad tas būs izdarīts.
Hei, tas bija ātri. Vai esat gatavs atbildei? Atšķirībā no dažiem vīrusu matemātikas problēmas kas ir tīri neskaidri un atvērti interpretācijai, šim patiesībā ir risinājums, kas neapšaubāmi ir par to, bez šaubām, par to, un tas ir 18. Dzirdēsim dažus ģeometrijas ekspertus par to, kāpēc.
"Es pietuvosos tam tāpat, kā pieeja jebkurai matemātiskai problēmai: samaziniet to un atrodiet struktūru," saka Sylvester Eriksson-Bique, Ph.D., pēcdoktorants kopā ar Kalifornijas Universitātes Losandželosas matemātiku nodaļa.
Vienīgais veids, kā veidot trijstūri manis zīmētajā attēlā, saka Ēriksons-Biskis, ir tad, ja augšējā virsotne (stūris) ir trijstūra daļa. Trīsstūra pamatnei tad jābūt vienam no trim līmeņiem. “Ir trīs līmeņi, un katrā no tiem varat izvēlēties bāzi no sešiem dažādiem veidiem. Tas dod 18 vai 3 reizes 6 trīsstūrus. ”
Apskatīsim galveno trijstūri vēlreiz.

Endrjū Danielss
“Ērti ir vispārināt to, kur ir n līnijas, kas šķērso augšējo virsotni, un lpp horizontālās līnijas, ”saka Fransisko Bonahons, Ph.D., Dienvidkalifornijas universitātes matemātikas profesors.
Mūsu gadījumā n = 4 un p = 3. Jebkuram trīsstūrī, ko atrodam zīmējumā, jābūt vienai augšējai virsotnei un divām citām virs tās pašas horizontālās līnijas, tāpēc katrai horizontālajai līnijai trijstūru skaits ar Bonahons saka, ka divas virsotnes šajā līnijā ir vienādas ar to, kā mēs varam izvēlēties šīs virsotnes, proti, cik daudz veidu mēs varam izvēlēties divus atšķirīgus punktus no nvai “n izvēlēties 2. ”
Vai atceries vidusskolas matemātiku? Tas ir n(n-1)/2. Un tā kā ir lpp horizontālas līnijas, saka Bonahana, tas dod p n(n-1) / 2 iespējamie trīsstūri. Mūsu gadījumā tas ir 3x4 (4-1) / 2 = 18.
Šis ir ērts sadalījums, kā atrast katru iespējamo trīsstūri:
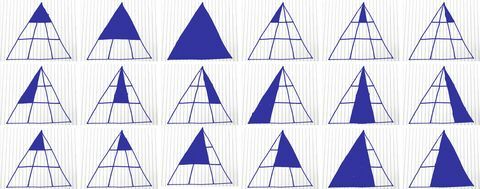
Korijs Kenedijs
Arī Buffalo universitātes matemātikas profesora asistente Johanna Mangahas, Ph. D., ieradās 18 gadu vecumā, vispirms izmantojot vienkāršu brutālā spēka skaitīšanu, pēc tam ar to pašu veiklo kombinatorika, kā minēts iepriekš, bet atzīst, ka mūsu trīsstūra smadzeņu ķircinātājs nav tik foršs kā šis no Po-Shen Loh, Ph. D., Karnegi Melona universitātes matemātikas profesora Pitsburga, kā parādīts Ņujorkas Laikspagājušais gads:
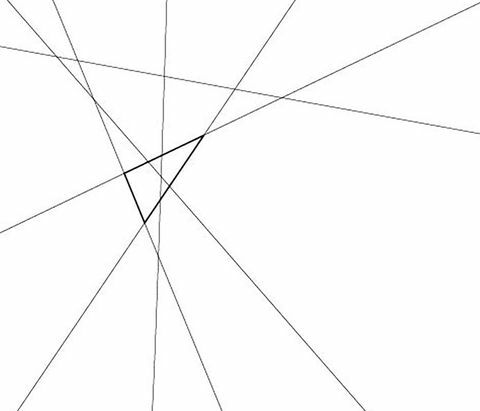
Po-Šen Lohs
Viņai ir matemātiska atbilde, kurā teikts: “Trijstūru skaitīšana ir tas pats, kas skaitīt trīs no sešām izvēlēto līniju kombinācijas [6-izvēlēties-3 = (6 * 5 * 4) / (3 * 2 * 1)].
"Tādā gadījumā katrs līniju pāris krustojas un nav trīskāršu vai vairāk krustojumu, tāpēc jebkura trīs izvēle vienmēr dod trīsstūri," saka Mangahas. Bildē, kuru viņai aizsūtīju, dažas līnijas ir paralēlas, tāpēc tās nevar būt viena un tā paša trīsstūra daļa. “Ja jūs izvēlētos tās pašas septiņas līnijas un mazliet tās satricinātu, iespējams, ka tās, visticamāk, būtu piezemējies kā [Lohs] problēma, un tev būtu vairāk trīsstūru un līdzīgas jaukas atbildes. ”(Ierakstam: 35.)
Kū. Es vēl neesmu dalījies ar šo jauno trīsstūra problēmu ar saviem kolēģiem. Bet tas ir tikai laika jautājums, pirms viņi to atklāj un argumentē vēl dažus.
🚨SVARĪGS ATJAUNINĀJUMS 1/30/20🚨: Kopš šī stāsta publicēšanas daudzi, daudzi lasītāji ir sazinājušies ar mani, ka, lai arī 18 gadi patiešām ir pieņemama atbilde uz šo problēmu, tā nav tikai viens, kas saistīts ar zināmu netīšu pārraudzību no manas puses. Es to būtu varējis daudz vieglāk izdarīt lasītājiem - un, kas ir izšķiroši, daudz vieglāk - iesūtnē, ja es tikko būtu ieskicējis trīsstūri uz vienkārša, balta datora papīra. Bet nē.
Diemžēl es uzzīmēju šo trīsstūri uz izklāta papīra, un daudzi gudri cilvēki ir pareizi norādījuši, ka patiesībā, ja attēlā saskaitāt gaiši zilas paralēlās līnijas papildus marķierā rakstītajām tumši zilajām līnijām, patiesībā šeit ir vairāk nekā 18 trīsstūri - ievērojami vairāk. Es nekad neesmu norādījis, ka jālieto tikai tās tumši zilās līnijas, un tāpēc es kļūdos. Tev ir taisnība.
Viens lasītājs Ralfs Linsangans man pilnībā piederēja, nosūtot šo attēlu, kurā viņš apzīmē katru papildu trīsstūri, kas atrasts zem tehniskā pamata, atzīmējot 17 papildu trīsstūrus, kopā 35. Lūk:
Šāda veida centība ir tikai viens no daudzajiem iemesliem, kādēļ es mīlu Populārā mehānika lasītājiem. Mēs neko nevaram paiet garām jums, puiši. Līdz nākamajam ķircinātājam!
🚨JEBKURS ATTIECĪBAS UZ Trīsstūra atjaunināšanu 1/31 / 20🚨: Kopš pēdējā atjauninājuma ievietošanas esmu dzirdējis no pat vairāk no tevis, turpinot mani un līdzcilvēkus lasīt, lai apsveru iespējamos papildu trīsstūrus. Uzklausīsim lasītāju Dereku Šneideru, kurš iesūtīja citu grafiku, kas liek domāt, ka ir 45 trīsstūri.
Tomēr, ja mēs ievērosim sākotnējos noteikumus, es skaita vēl 9 un tos, kas ir noteikti (zaļā krāsā) un kurus varētu esiet atvērts interpretācijai atkarībā no tā, kā jūs vizuāli novietojat virsotni (purpursarkanā krāsā)… Es personīgi skaitītos tā.

Dereks Šneiders
Lasītājs Poingijs tikmēr rakstīja, ka ir izdarījis “nopietnu kļūdu”, saskaitot trīsstūrus visā garumā:
Ņemiet, piemēram, apakšējo labo stūri, tas parāda vienu bultiņu vienam trīsstūrim. Tomēr šīs gaiši zilās līnijas, iespējams, varētu veidot pat trīs Trīsstūrus tikai šajā vienā stūrī:

Poying
Kaut arī daži no tiem VAR būt nedaudz diskutabli (ti, kur tieši Gaiši zilas līnijas krustojas ar tumšām un tie tehniski veido trīsstūri vai četrstūri), es esmu saskaitījis SEPTUS PAPILDUS trijstūrus, ko var izveidot šajā veids. Tādējādi kopējais trijstūru skaits var sasniegt 42.
Sliktā ziņa ir tā, ka mēs nokavējām dažus trīsstūrus. Labā ziņa ir tā, ka tas apstiprina, ka dzīvei acīmredzami ir jēga, par ko liecina precīzs skaits: 42.
Izcils punkts, Poying. Lasītājs Džeimss Goodrihs paspēra to vēl vienu soli tālāk, iesakot mums atvērt prātu, lai pārdomātu, kāds varētu būt trīsstūris:
Nu, kā norāda jūsu lasītājs, kurš norādīja uz 17 papildu trīsstūriem (izmantojot taustiņu “Endrjū to nedarīja norādiet, kādas līnijas var ietvert klauzulas 3 trīsstūra malas), neizdevās skaidri atrast diezgan daudz vairāk. Piemēram, paņemiet apakšējo kreiso mini trīsstūri 2020. gada 30. janvāra papildinājumā “Svarīgs atjauninājums”. Vai mini-trīsstūra laukumi un tam blakus esošā romba laukumi apvienoti neveidotu citu trīsstūri?
Vēl viena ideja, kas jāņem vērā: trīsstūriem ir 3 leņķi (kurš gan būtu uzminējis?); tomēr es postulētu, ka tas, kā jūs aprakstāt trīsstūri, izmantojot minētos leņķus, radītu dažādus trīsstūrus. Ņemot vērā trīsstūri T ar virsotnēm A, B un C, t-vienu patiešām var aprakstīt ar ABC, B ir centrālais leņķis. Es ierosinu, ka t-divi, kurus apraksta BAC, ir atšķirīgi. Līdzīgi arī BCA.
Ja mēs ņemam vērā konkrētu gadījumu, taisna leņķa trīsstūrus, mēs varam iegūt sinusa, kosinusa un tangentes funkcijas (SOH, CAH, TOA). Ja mēs to piemērotu trīsstūrim (un atslābinātu taisnleņķa prasību, tas varētu nozīmēt, ka BAC atšķiras no CAB. Protams, izņēmumi tiek izdarīti izoskoles un vienādmalu trīsstūriem (pēdējiem būtu tikai 3 atšķirīgas trīsstūra definīcijas).
Es vēl neesmu īsti domājis, kā kvantitatīvi izteikt katru ierosinājumu (un, piemērojot pēdējo pēc pirmā, tas pieaugtu joprojām), tāpēc man nav vienkārša numura, kuru jūs varētu izmantot atjauninātajā svarīgajā atjauninājumā (ja atradāt manas idejas, kuras būtu vērts izmantot) Atjaunināt).
Es to izdarīju, Džeimss. Un es gaidīšu. Beidzot, es nolēmu veikt pēdējos vilcienus, lai noskaidrotu, cik papildu trijstūriem varētu dot mūsu jaunos haotiskos likumus, un nonācu pie 43, kopā 61:
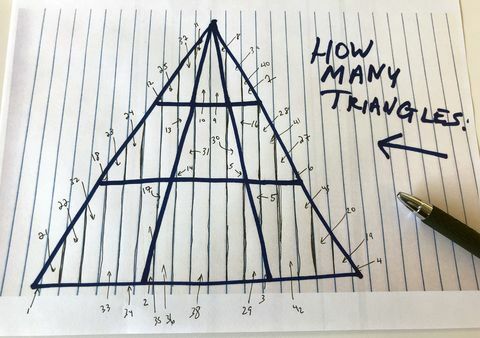
Endrjū Danielss
Es tomēr esmu pilnīgi pārliecināts, ka kāds, kas to lasīs, ļoti ātri man pateiks, ka es atkal kļūdos, un iesniegs pierādījumus vēl vairāk slēptu trīsstūru, nosūtot man vēl vienu truša caurumu uz garā un līkumainā ceļa uz iespējamo ārprāts. (Piezīme: Es savu sievu neesmu redzējis trīs dienu laikā. Lūdzu, pasakiet viņai, ka es viņu mīlu.) Tāpēc es izdodu vēl vienu izaicinājumu: Ja oriģinālajā attēlā varat atrast iespējami trīsstūrus, parādiet man savu darbu un noteikti pierādiet jūsu pārākums, es pēdējo reizi atjaunināšu šo stāstu un vainagosim jūs par trīsstūra karali vai karalieni tagad un mūžīgi. Dievspēks.

SpeedRipper Rubika kubs
$12.45
Rubika kubs 40 gadus ir satracinājis cilvēkus. Mēģiniet pats to izdomāt, vai iemācīties to atrisināt izmantojot matemātiku.

Kanoodle trīsdimensiju spēle
$8.79
Kanoodle ir tikai 12 skaņdarbi, bet kopā ir 200 izaicinājumu, bet gan bērnus, gan pieaugušos ar 2-D un 3-D mīklām.

Galda spēle Sagrada
$29.98
Vienā no labākajām mīklām gada galda spēles, jūs un vēl trīs spēlētāji mēģināt izgatavot Sagrada Familia vitrāžas.

3D dimensijas puzzle spēle
$40.97
Šī ātrdarbīgā trīsdimensiju puzzle spēle ietver ātru domāšanu, loģiku un veiksmi kombinācijā ar sfērām, lai nopelnītu visvairāk punktu.
No:Populārā mehānika


